BFS used in problem 8 numbers

“8 numbers problem” in CPII 2020 Spring: solution and some related basic knowledge used in it.

Preknowledge

BFS（广度优先搜索）

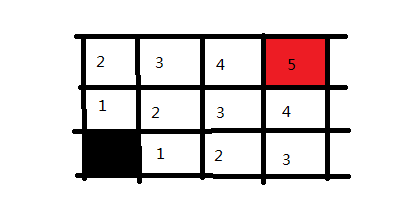
广度优先搜索较之深度优先搜索之不同在于，深度优先搜索旨在不管有多少条岔路，先一条路走到底，不成功就返回上一个路口然后就选择下一条岔路，而广度优先搜索旨在面临一个路口时，把所有的岔路口都记下来，然后选择其中一个进入，然后将它的分路情况记录下来，然后再返回来进入另外一个岔路，并重复这样的操作，用图形来表示则是这样的，例子:

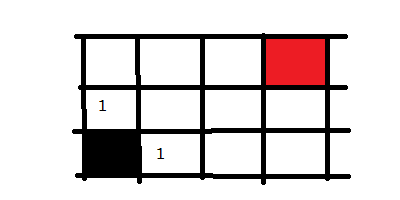
从黑色起点出发，记录所有的岔路口，并标记为走一步可以到达的。然后选择其中一个方向走进去，我们走黑点方块上面的那个，然后将这个路口可走的方向记录下来并标记为2，意味走两步可以到达的地方。

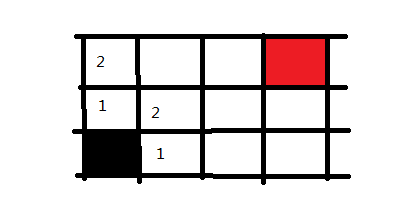
接下来，我们回到黑色方块右手边的1方块上，并将它能走的方向也记录下来，同样标记为2，因为也是走两步便可到达的地方

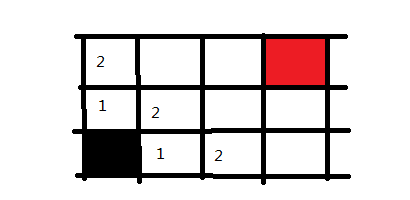
这样走一步以及走两步可以到达的地方都搜索完毕了，下面同理，我们可以迅速把三步的格子给标记出来

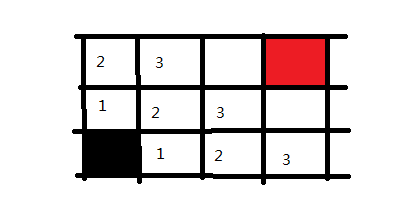
再之后是四步，五步。

我们便成功寻找到了路径，并且把所有可行的路径都求出来了。在广度优先搜索中，可以看出是逐步求解的，反复的进入与退出，将当前的所有可行解都记录下来，然后逐个去查看。在DFS中我们说关键点是递归以及回溯，在BFS中，关键点则是状态的选取和标记。
int n = 10, m = 10;                   //地图宽高
void BFS()
{
    queue que;              //用队列来保存路口
    int graph[n][m];          //地图
    int px[] = {-1, 0, 1, 0};   //移动方向的数组
    int py[] = {0, -1, 0, 1};
    que.push(起点入队);      //将起点入队
    while (!que.empty()) {    //只要队列不为空
        auto temp = que.pop();          //得到队列中的元素
        for (int i = 0; i != 4; ++i) {
            if(//可以走) {
                //标记当前格子
                //将当前状态入队列，等待下次提取
            }
        }
    } 
}
注：以上两个代码只是提供思路，并非是语法正确的可运行代码。

总结

对于这两个搜索方法，其实我们是可以轻松的看出来，他们有许多差异与许多相同点的。

1.数据结构上的运用

DFS用递归的形式，用到了栈结构，先进后出。

BFS选取状态用队列的形式，先进先出。

2.复杂度

DFS的复杂度与BFS的复杂度大体一致，不同之处在于遍历的方式与对于问题的解决出发点不同，DFS适合目标明确，而BFS适合大范围的寻找。

3.思想

思想上来说这两种方法都是穷竭列举所有的情况。

From: Zhihu: Linkcheng

Cantor 展开

Target usage

Cantor 展开用于求解一个全排列的序号。例如：12345 序号为 1 ，12354 序号为 2，按字典序增加序号递增。 Cantor 逆展开用于求解序号对应的排列。

Explanation

康托展开的基本公式如下： $X=a_n(n-1)!+a_{n-1}(n-2)!+···+a_1\times0!+1$

其中X代表该排列的排名， $a_i$ 代表该排列中的第i位数字在第i位其后的数字中按升序排在第几个（以0为最小）。

举个例子：在1~5的排列中，求解34152的排名。

第1位数字是3，在34152中按升序排在第2个。（最小的是第0个）故 $a_1=2。$

第2位数字是4，在4152中按升序排在第2个。 $a_2=2$

第3位数字是1，在152中按升序排在第0个。 $a_3=0$

第4位数字是5，在52中按升序排在第1个。 $a_4=1$

最后一位 $a_5$ 固定为0。

则 $X=2\times(5-1)!+2\times(5-2)!+0\times(5-3)!+1\times(5-4)!+0\times(5-5)!+1=62$

字典序

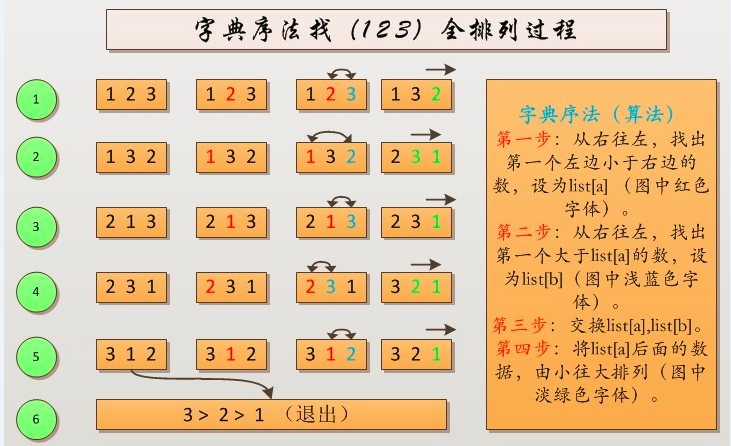
811207-20160316224604443-404581276

8 numbers problem

Content

3×3九宫棋盘，放置数码为1-8的8个棋牌，剩下一个空格，只能通过棋牌向空格的移动来改变棋盘的布局。要求：根据给定初始布局，问：至少移动几次才能从初始布局到达目标布局。

目标布局如下图：

8 7 6 5 4 3 2 1

Input Description

3行，每行3个0-8的不重复整数，其中0表示空格所在的位置，数字间用空格隔开，表示初始布局，数据保证该初始布局一定能移到目标布局。

Output Description

一个整数，表示最少移动到目标布局的次数。

Sample

INPUT

0 7 6 8 4 3 5 2 1

OUTPUT

Main method

对于每种情况，可以看作 9 个数字的不同排列，也就是说会有 9！=362880 种情况，而每种情况用一个字符串进行记录，也方便调用字符串函数减少工作量。为了避免搜索重复情况，将建立一个 HASH 表。每种排列的 Cantor 展开是唯一的，故可以此作为对应关系。

每种状态的记录以及挪动元素的实现

记录

例如：将 INPUT 情况记作序列

int arr[9] = {0,7,6,8,4,3,5,2,1}

挪动元素

那么对于其中某一个元素（如 8 ）向上一格，只需令 8 与它之前的第三个元素进行交换，同时需要满足：

之前的第三个元素是 0；只需
```
arr[where_8_is_located - 3] = 0
```
不在边缘。可以用标记该位置是否可以向左移动实现。
```
int mobility[9][4]={ {0,1,0,1},{0,1,1,1},{0,1,1,0},{1,1,0,1},{1,1,1,1},{1,1,1,0},{1,0,0,1},{1,0,1,1},{1,0,1,0} }  //order in up, down, left and right, 0 means unable;
```
同理，向左一格是与该元素之前的一个元素进行交换…

避免重复搜索

原 Blog 中利用 Hash 表 + Cantor 展开. 复习一下上面的公式和算法：（似乎是我自己记不住… ） $X=a_n(n-1)!+a_{n-1}(n-2)!+···+a_1\times0!+1$

其中X代表该排列的排名， $a_i$ 代表该排列中的第i位数字在第i位其后的数字中按升序排在第几个（以0为最小）。

int cantor(char x[],int n)  // calculate the cantor function 
{
	int fac[]={1,1,2,6,24,120,720,5040,40320};  // values of factorial, from 0 to 8 (there is 9 numbers used in total) 
	int i,j,num=0,count; //num means X.
	for(i=0;i<n;i++)
	{
		count=0;
		for(j=i+1;j<n;j++)
			if(x[j]<x[i]) count++;
		
		num+=count*fac[n-1-i];
	}
	return num + 1;
}

Write-up

#include <stdio.h>
#include <string.h>
#define MAX 400000  // all of the possible routes 9! = 362880

int hash [MAX];  
char aim[10]="876543210";
char single_status [MAX][10]; // every single status. 9! in total

int cantor(char x[],int n)  // calculate the cantor function 
{
	int fac[]={1,1,2,6,24,120,720,5040,40320};  // values of factorial, from 0 to 8 (there is 9 numbers used in total) 
	int i,j,num=0,count; //num means X.
	for(i=0;i<n;i++)
	{
		count=0;
		for(j=i+1;j<n;j++)
			if(x[j]<x[i]) count++;
		
		num+=count*fac[n-1-i];
	}
	return num + 1;
}

int bfs(int p, int q, int n){
    int i,j=q+1,t,num;
    char new_status[10]; // new status

    for(i=p;i<=q;i++){
        if(strcmp(single_status[i],aim)==0){
            printf("%d",n);
            return 0;
        }

        t=0;
        while(single_status[i][t]!='0'){
            t++;
        }
        if(t>2){ // 0 isn't in the first line
        strcpy(new_status,single_status[i]);
        new_status[t]=single_status[i][t-3];// down
        new_status[t-3]=single_status[i][t];
        num = cantor(new_status,9);
        if(hash[num]==1){
            strcpy(single_status[j],new_status);
            hash[num] = 0;
            j++;
        }
        }
        if(t<6){
        strcpy(new_status,single_status[i]);
        new_status[t]=single_status[i][t+3];// down
        new_status[t+3]=single_status[i][t];
        num = cantor(new_status,9);
        if(hash[num]==1){
            strcpy(single_status[j],new_status);
            hash[num] = 0;
            j++;
        }
        }
        if(t%3 != 0){
        strcpy(new_status,single_status[i]);
        new_status[t]=single_status[i][t-1];// down
        new_status[t-1]=single_status[i][t];
        num = cantor(new_status,9);
        if(hash[num]==1){
            strcpy(single_status[j],new_status);
            hash[num] = 0;
            j++;
        }
        }
        if(t%3 != 2){
        strcpy(new_status,single_status[i]);
        new_status[t]=single_status[i][t+1];// down
        new_status[t+1]=single_status[i][t];
        num = cantor(new_status,9);
        if (hash[num] == 1) {
          strcpy(single_status[j], new_status);
          hash[num] = 0;
          j++;
        }
        }
        
    }
    bfs(q + 1, j - 1, n + 1);
    return 0;
}
int main(){
    int i,trans;
    for(i = 0;i<9;i++){
        scanf("%d",&trans);
        single_status[0][i]=trans+'0';
    }
    single_status[0][9]='\0';
    for(i = 0;i<MAX;i++){
        hash[i]=1;
    }
    hash[cantor(single_status[0],9)]=0;
    bfs(0,0,0);
    return 0;
}

Share on

Twitter Facebook LinkedIn